TUTORS AV
Enchancing the learning experience

---

HOME	POST A QUESTION	ANSWERED QUESTIONS	FEEDBACK

1. Why is it that (xy)^-1 = x^-1y^-1?(Mathematics)
   Asked by: Aastha Posted on: 30/05/2013
2. How many minutes past 11AM is it if two hours ago it was three times as many minutes, past 8AM?(Mathematics)
   Asked by: Miss Posted on: 23/05/2013
3. List the ways in which 7 / 12 can be written as a sum of two fractions in lowest terms such that the denominators of the two fractions are different and neither of them is more than 12.(Mathematics)
   Asked by: Miss Posted on: 23/05/2013
4. By using four 3's with the mathematical operators ( + , - , / , * ) obtain the results 0, 1, 2 and 3.(Mathematics)
   Asked by: Miss Posted on: 23/05/2013
5. By using four 4's along with any mathematical operator, make a total of 420.(Mathematics)
   Asked by: Miss Posted on: 23/05/2013
6. Find the values of sin(x/2), cos(x/2) and tan(x/2) if tan(x)=-4/3.(Mathematics)
   Asked by: Ayan Posted on: 15/05/2013
7. Prove that (cos2θ)(3+cos4θ) = 4(cos⁸θ-sin⁸θ).(Mathematics)
   Asked by: Ayan Posted on: 28/04/2013
8. If Set A has 3 elements and Set B has 6 elements, prove that the minimum and maximum number of elements in A∪B is 6 and 9 respectively.(Mathematics)
   Asked by: Yash Posted on: 27/04/2013
9. If n(U)=500, n(F)=285, n(H)=195, n(B)=115, n(F∩B)=45, n(F∩H)=70, n(H∩B)=50, n(H∪B∪F)’=50, then find n(H∩B∩F) and n(H-B-F) + n(B-F-H) + n(F-B-H).(Mathematics)
   Asked by: Yash Posted on: 27/04/2013
10. If n(M∪B)=25, n(M)=12, n(M-B)=8, then find n(B-M) and n(B∩M).(Mathematics)
    Asked by: Yash Posted on: 27/04/2013
11. If n(U)=10000, n(A)=4000, n(B)=2000, n(C)=1000, n(A∩C)=400, n(A∩B)=500, n(B∩C)=300, n(A∩C∩B)=200, then find n(A-B-C) and n(A∪B∪C)’.(Mathematics)
    Asked by: Yash Posted on: 27/04/2013
12. If If n(U)=200, n(M)=120, n(P)=90, n(C)=70, n(M∩C)=50, n(M∩P)=40, n(P∩C)=30, n(P∪C∪M)’=20, then find n(M∩C∩P).(Mathematics)
    Asked by: Yash Posted on: 27/04/2013
13. If n(U)=60, n(C)=25, n(T)=20, n(C)=11, n(T∩C)=10, then find n(T∪C)’.(Mathematics)
    Asked by: Yash Posted on: 27/04/2013
14. If n(U)=25, n(M)=15, n(P)=12, n(C)=11, n(M∩C)=5, n(M∩P)=9, n(P∩C)=4, n(M∩C∩P)=3, then find n(C-P-M), n(M-C-P), n(P-M-C), n((P∩C)-M), n((P∩M)-C), n(C-P-M) + n(M-C-P) + n(P-M-C), n(P∪C∪M), n(P∪C∪M)’.(Mathematics)
    Asked by: Yash Posted on: 27/04/2013
15. If |(z+i5)/(z-i5)| = 1, then prove z is purely real.(Mathematics)
    Asked by: Harsh Posted on: 25/04/2013
16. How many moles and grams of NaCl are present in 250cm³ of 0.5 molar NaCl solution?(Chemistry)
    Asked by: Miss Posted on: 24/04/2013
17. Concentration of H₂SO₄ in its aqueous solution is 98 % by mass and the solution has a density of 1.84g/cm³. What volume of the solution is required to make 5L of 0.5 molar H₂SO₄ solution?(Chemistry)
    Asked by: Miss Posted on: 24/04/2013
18. Calculate the area under the curve f(x) = e^-x bounded by the positive x and y axes.(Mathematics)
    Asked by: Ayan Posted on: 23/04/2013
19. In three moles of ethane, calculate the number of moles of carbon atoms.(Chemistry)
    Asked by: Tanushree Posted on: 22/04/2013
20. What is the number of atoms in 52u of Helium?(Chemistry)
    Asked by: Tanushree Posted on: 22/04/2013
21. What will be the mass of one atom of Carbon 12 isotope in grams?(Chemistry)
    Asked by: Tanushree Posted on: 22/04/2013
22. What are pyrenoids?(Biology)
    Asked by: Arvind Posted on: 04/04/2013
23. Two APs have the same common difference. The first term of one AP is 2 and that of the other is 7. The difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms. Why?(Mathematics)
    Asked by: Miss Posted on: 07/03/2013
24. The location of a dot P at a given time t in the xy plane is given by (x,y) = (t−sint,1−cost). What is the distance traveled by P in the interval 0≤t≤2π?(Mathematics)
    Asked by: Miss Posted on: 06/03/2013
25. A man is employed to count Rs 10710. He counts at the rate of Rs 180 per minute for half an hour. After this he counts at the rate of Rs 3 less every minute than the preceding minute. Find the time taken by him to count the entire amount.(Mathematics)
    Asked by: Miss Posted on: 06/03/2013
26. A tank, internally measuring 150cm x 120cm x 110cm, has 129600 cubic cm of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in it without overflowing the water, each brick having dimensions 22.5cm x 7.5cm x 6.5cm?(Mathematics)
    Asked by: Miss Posted on: 06/03/2013
27. An AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the last three is 429. Find the AP.(Mathematics)
    Asked by: Miss Posted on: 05/03/2013
28. A boy standing on the ground and flying a kite with 120m of string at an angle of 30. Another boy standing on the roof of a 14m high building and is flying his kite at an angle of elevation of 45. Both boys are standing opposite of both the kites. Find the length of the string that the second boy must have so that the two kites meet. (Mathematics)
    Asked by: Miss Posted on: 05/03/2013
29. The ratio of sum of n terms of two AP's is (7n+1):(4n+27). Find the ratio of their mth terms.(Mathematics)
    Asked by: Miss Posted on: 05/03/2013
30. The sum the first p,q,r terms of an AP are a,b,c respectively. Show that a(q-r)/p + b(r-p)/q + c(p-q)/r = 0.(Mathematics)
    Asked by: Miss Posted on: 05/03/2013
31. If √2cosθ - √6sinθ = 2√2. Find θ.(Mathematics)
    Asked by: Miss Posted on: 05/03/2013
32. A right triangle whose sides are 3cm,4cm and 5cm is revolved about the sides containing the right angle in two ways. Find the difference of volumes of the cones so formed.(Mathematics)
    Asked by: Miss Posted on: 04/03/2013
33. Find the 101st term of the sequence : 4,7,12,19 ................(Mathematics)
    Asked by: Miss Posted on: 04/03/2013
34. A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.(Mathematics)
    Asked by: Miss Posted on: 04/03/2013
35. What is the area of the sector of a circle of radius 5cm, which is formed by an arc of length 3.5cm?(Mathematics)
    Asked by: Miss Posted on: 04/03/2013
36. Seven years ago Varun's age was five times the square of Swati's age. Three years hence Swati's age will be two fifth of Varun's age. Find their present ages.(Mathematics)
    Asked by: Miss Posted on: 04/03/2013
37. For what values of k does kx²+12x+9=0 have imaginary roots?(Mathematics)
    Asked by: Miss Posted on: 04/03/2013
38. A chord of length 10 cm divides a circle of radius 5√2 cm in two segments. Find the area of minor segment.(Mathematics)
    Asked by: Miss Posted on: 03/03/2013
39. A solid cone of base radius 10cm is cut into two parts through mid points of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.(Mathematics)
    Asked by: Miss Posted on: 03/03/2013
40. While boarding an aeroplane a passenger got hurt. The pilot showing promptness and concern made arrangements to hospitalise the injured and so the plane started late by 30 min. To reach the destination 1500 km away in time, the pilot increased the speed by 100 km/hr. Find the original speed/hour of the plane.(Mathematics)
    Asked by: Miss Posted on: 03/03/2013
41. In a figure O is the centre of a circle. PA and PB are tangents forom an external point P touching the circle at points A and B. If OP is equal to the diameter then prove that ABP is an equilateral triangle.(Mathematics)
    Asked by: Miss Posted on: 03/03/2013
42. The 19th term of an AP is equal to three times its sixth term. If its 9th term is 19,find the AP.(Mathematics)
    Asked by: Miss Posted on: 03/03/2013
43. There are 3 villages A,B and C such that the distance from A to B is 7Km, from B to C is 5 Km and from C to A is 8 Km. The gram pradhan wants to dig a well in such a way that the distance from each villages are equal. What should be the location of well?(Mathematics)
    Asked by: Miss Posted on: 03/03/2013
44. ABCD is a square with one side equal to 7cm. It consists of two quadrants ABC and BCD. Their point of intersection is P. Find the area of the shaded region.(Mathematics)
    Asked by: Ayan Posted on: 02/03/2013
45. The sum of first q terms of an AP is 63q-3q² .If its pth term is -60,find the value of p. Also,find the 11th term of this AP.(Mathematics)
    Asked by: Miss Posted on: 02/03/2013
46. Two water taps together can fill a tank in 75/8 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.(Mathematics)
    Asked by: Rishabh Posted on: 25/02/2013
47. How can I unlock Legendary difficulty level in MotoGP2?(Gaming)
    Asked by: Prateek Posted on: 25/02/2013
48. Solve for x: 1/(x-1)(x-2) + 1/(x-2)(x-3) + 1/(x-3)(x-4) = 1/16.(Mathematics)
    Asked by: Arjun Posted on: 25/02/2013
49. If a/(a+b) = 15/21, then find (a+b)/(a-b).(Mathematics)
    Asked by: Pallavi Posted on: 24/02/2013
50. If the weight of a bucket full of water is 24 kg and weight of the bucket 1/4th full of water is 9 kg, then find the weight of the empty bucket.(Mathematics)
    Asked by: Pallavi Posted on: 24/02/2013
51. If the mean weight of 8 people is increased by 4 when a person of weight 30 kg is replaced by another man, find the weight of the new man.(Mathematics)
    Asked by: Pallavi Posted on: 24/02/2013
52. It is proposed to add to a square lawn measuring 58 m on a side, two circular ends.The center of each circle being the point of intersection of the diagonals of the square.Find the area of the whole lawn. (Mathematics)
    Asked by: Irene Posted on: 23/02/2013
53. What should be the position of an object relative to biconvex lens so that the lens behaves like a magnifying glass?(Physics)
    Asked by: Vyomika Posted on: 22/02/2013
54. Find the sum of all three digits numbers each of which leave the remainder 3 when divided by 5.(Mathematics)
    Asked by: Vyomika Posted on: 22/02/2013
55. For what value of 'K' the numbers 3K + 2, 4K + 3 and 6K - 1 are the consecutive terms of an AP?(Mathematics)
    Asked by: Vyomika Posted on: 22/02/2013
56. If an aeroplane is flying horizontally at a height of 'h' meters from the ground and the angle of depressions of two consecutive kilometer stones(which are on either sides of the aeroplane) from the it are 'A' and 'B'. Then prove that: h = (tanA.tanB)/(tanA + tanB).(Mathematics)
    Asked by: Arjun Posted on: 22/02/2013
57. What is catenation?(Chemistry)
    Asked by: Sushant Posted on: 20/02/2013
58. Coding of internal linking(Computer Science)
    Asked by: Ayan Posted on: 19/02/2013
59. Coding of external linking(Computer Science)
    Asked by: Ayan Posted on: 19/02/2013
60. What was the name of the first dog sent to the moon?(General Knowledge)
    Asked by: Anand Posted on: 15/02/2013
61. The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?(Mathematics)
    Asked by: Sagar Posted on: 09/02/2013
62. The mean of 5 numbers is 18. If one of the numbers is excluded, their mean is 16. Then the excluded number is ___?(Mathematics)
    Asked by: Sagar Posted on: 09/02/2013
63. Find the co-ordinates of the point at which the perpendicular bisector of the line segment joining the points (1,5) and (4,6) cuts the y-axis.(Mathematics)
64. If z = x + iy, then |2z - i| / |z + 1| = m represents a circle when m is not equal to ____?(Mathematics)
    Asked by: Kanishkh Posted on: 16/01/2013

Question

Why is it that (xy)^-1 = x^-1y^-1?

Answer:

We know that any number raised to -1 is its reciprocal.
Therefore, we have (xy)^-1 = 1/xy which is equal to (1/x)*(1/y).
We see that the result is the product of the reciprocals of x and y and therefore we can also write it as x^-1y^-1.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

How many minutes past 11AM is it if two hours ago it was three times as many minutes, past 8AM?

Answer:

It is 30 minutes past 11AM.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

List the ways in which 7 / 12 can be written as a sum of two fractions in lowest terms such that the denominators of the two fractions are different and neither of them is more than 12.

Answer:

1/2+1/12; 1/3+1/4; 1/6+5/12.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

By using four 3's with the mathematical operators ( + , - , / , * ) obtain the results 0, 1, 2 and 3.

Answer:

The results are given below.

3+3-3-3=0
(3/3)+3-3=1
(3/3)+(3/3)=2
(3+3+3)/3=3


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

By using four 4's along with any mathematical operator, make a total of 420.

Answer:

444 - 4!

Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Find the values of sin(x/2), cos(x/2) and tan(x/2) if tan(x)=-4/3.

Answer:

sin(x/2)=2√5/5, cos(x/2)=√5/5 and tan(x/2)=2.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Prove that (cos2θ)(3+cos4θ) = 4(cos⁸θ-sin⁸θ).

Answer:

The proof is given below.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If Set A has 3 elements and Set B has 6 elements, prove that the minimum and maximum number of elements in A∪B is 6 and 9 respectively.

Answer:

The proof is given below.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If n(U)=500, n(F)=285, n(H)=195, n(B)=115, n(F∩B)=45, n(F∩H)=70, n(H∩B)=50, n(H∪B∪F)’=50, then find n(H∩B∩F) and n(H-B-F) + n(B-F-H) + n(F-B-H).

Answer:

Values of n(H∩B∩F) and n(H-B-F) + n(B-F-H) + n(F-B-H) are 20 and 325 respectively.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If n(M∪B)=25, n(M)=12, n(M-B)=8, then find n(B-M) and n(B∩M).

Answer:

Values of n(B-M) and n(B∩M) are 13 and 4 respectively.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If n(U)=10000, n(A)=4000, n(B)=2000, n(C)=1000, n(A∩C)=400, n(A∩B)=500, n(B∩C)=300, n(A∩C∩B)=200, then find n(A-B-C) and n(A∪B∪C)’.

Answer:

Values of n(A-B-C) and n(A∪B∪C)’ are 3300 and 4000 respectively.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If If n(U)=200, n(M)=120, n(P)=90, n(C)=70, n(M∩C)=50, n(M∩P)=40, n(P∩C)=30, n(P∪C∪M)’=20, then find n(M∩C∩P).

Answer:

Value of n(M∩C∩P) is 20.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If n(U)=60, n(C)=25, n(T)=20, n(C)=11, n(T∩C)=10, then find n(T∪C)’.

Answer:

Value of n(T∪C)’ is 25.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If n(U)=25, n(M)=15, n(P)=12, n(C)=11, n(M∩C)=5, n(M∩P)=9, n(P∩C)=4, n(M∩C∩P)=3, then find n(C-P-M), n(M-C-P), n(P-M-C), n((P∩C)-M), n((P∩M)-C), n(C-P-M) + n(M-C-P) + n(P-M-C), n(P∪C∪M), n(P∪C∪M)’.

Answer:

The answers are given below.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If |(z+i5)/(z-i5)| = 1, then prove z is purely real.

Answer:

The proof is given below.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

How many moles and grams of NaCl are present in 250cm³ of 0.5 molar NaCl solution?

Answer:

There are 1/8 moles or 7.31 grams of NaCl present in the solution.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Concentration of H₂SO₄ in its aqueous solution is 98 % by mass and the solution has a density of 1.84g/cm³. What volume of the solution is required to make 5L of 0.5 molar H₂SO₄ solution?

Answer:

135.87 mL of the solution is required.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Calculate the area under the curve f(x) = e^-x bounded by the positive x and y axes.

Answer:

The area is 1 square units.

We have to calculate area under the curve bounded by the positive x and y axes.
So, x varies from 0 to ∞.
Therefore, we have to find ∫e^-xdx when x varies from 0 to ∞.
To find the integral of e^-x, we find a function whose derivative is e^-x. Thus, we get ∫e^-xdx = -e^-x.
Therefore, the area under the curve
= -e^-∞ - (-e⁰)
= 0 + 1
= 1 sq. unit


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

In three moles of ethane, calculate the number of moles of carbon atoms.

Answer:

The number of moles of carbon atoms in ethane is 6.

As we know that the molecular formula of ethane is C₂H₆, we come to know that 1 molecule of ethane contains 2 atoms of carbon.
Therefore, 1 mole of ethane molecules will contain 2 moles of carbon atoms and so 3 moles of ethane molecules will contain 3*2 = 6 moles of carbon atoms.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

What is the number of atoms in 52u of Helium?

Answer:

13 atoms are present in 52u of Helium.

We know that the atomic mass of Helium = 4u
Therefore, in 4u of Helium, 1 atom is present and so, in 4*13 = 52u of Helium, we will have 1*13 = 13 atoms.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

What will be the mass of one atom of Carbon 12 isotope in grams?

Answer:

Mass of one atom of C-12 isotope is 1.99269*10^-23 grams.

We know that the atomic mass of carbon-12 = 12u
Therefore, molar mass of carbon = 12g
Number of carbon atoms in 1 mole of carbon = 6.022*10²³
Therefore, we can say that mass of 6.022*10²³ atoms of carbon is 12g and so 1 atom of carbon have mass equal to 12/(6.022*10²³) = 1.99269*10^-23 grams.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

What are pyrenoids?

Answer:

Pyrenoids are organelles found in algae and hornwarts(non vascular plants) and they serve as the centers for CO₂ fixation. Pyrenoids are not membrane-bound, but specialized areas of the plastid that contain high levels of ribulose-1,5-bisphosphate carboxylase/oxygenase.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Two APs have the same common difference. The first term of one AP is 2 and that of the other is 7. The difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms. Why?

Answer:

The reason is given below.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

The location of a dot P at a given time t in the xy plane is given by (x,y) = (t−sint,1−cost). What is the distance traveled by P in the interval 0≤t≤2π?

Answer:

The distance traveled by the point is 2π units.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A man is employed to count Rs 10710. He counts at the rate of Rs 180 per minute for half an hour. After this he counts at the rate of Rs 3 less every minute than the preceding minute. Find the time taken by him to count the entire amount.

Answer:

He take 89 minutes or 1 hour and 29 minutes to count the whole sum.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A tank, internally measuring 150cm x 120cm x 110cm, has 129600 cubic cm of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in it without overflowing the water, each brick having dimensions 22.5cm x 7.5cm x 6.5cm?

Answer:

1792 bricks can be put in the tank.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

An AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the last three is 429. Find the AP.

Answer:

The AP is 3,7,11,15,.......

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A boy standing on the ground and flying a kite with 120m of string at an angle of 30. Another boy standing on the roof of a 14m high building and is flying his kite at an angle of elevation of 45. Both boys are standing opposite of both the kites. Find the length of the string that the second boy must have so that the two kites meet.

Answer:

The length of the string is 46√2m.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

The ratio of sum of n terms of two AP's is (7n+1):(4n+27). Find the ratio of their mth terms.

Answer:

The ratio of their mth terms is 7:4.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

The sum the first p,q,r terms of an AP are a,b,c respectively. Show that a(q-r)/p + b(r-p)/q + c(p-q)/r = 0.

Answer:

The proof is shown below.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If √2cosθ - √6sinθ = 2√2. Find θ.

Answer:

θ = -60.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A right triangle whose sides are 3cm,4cm and 5cm is revolved about the sides containing the right angle in two ways. Find the difference of volumes of the cones so formed.

Answer:

Difference of their volumes is 4π cubic cm.

Case 1(The triangle is revolved about the side of length 3cm):
The height of the cone becomes 3cm and the base radius becomes 4cm.
Case 2(The triangle is revolved about the side of length 4cm):
The height of the cone becomes 4cm and the base radius becomes 3cm.
Therefore, the difference of their volumes:
= (1/3)π*3*3*4 - (1/3)π*4*4*3
= (1/3)π*4*3(4-3) [Taking (1/3)π*4*3 common]
= 4π*1 = 4π cubic cm.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Find the 101st term of the sequence : 4,7,12,19 ................

Answer:

The 101st term of the sequence is 10204.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.

Answer:

Area of the square plot is 2.1404 hectares.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

What is the area of the sector of a circle of radius 5cm, which is formed by an arc of length 3.5cm?

Answer:

Area of the sector is 8.75 sq cm.

We are given that the length of the arc is 3.5 cm and the radius of the circle is 5 cm.
Therefore,
2πr*θ/360 = 3.5
⇒ 2πr*(θ/360)*r/2 = 3.5*r/2 (Multiplying both sides by r/2)
⇒ πr²(θ/360) = 3.5*2.5 = 8.75 sq cm
As we know πr²(θ/360) is the area of a sector with angle θ, we can conclude that area of the sector is 8.75 sq cm.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Seven years ago Varun's age was five times the square of Swati's age. Three years hence Swati's age will be two fifth of Varun's age. Find their present ages.

Answer:

Varun's present age is 27 years and Swati's present age is 9 years.

Click on the picture for an enlarged view.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

For what values of k does kx²+12x+9=0 have imaginary roots?

Answer:

K is greater than 4.

For the given equation to have imaginary roots, the discriminant has to be negative.
Therefore,
D = b² - 4ac < 0
⇒ 12² - 4(k)(9) < 0
⇒ 144 - 36k < 0
⇒ 144 < 36k
⇒ 144/36 < k
⇒ 4 < k
Therefore, for all values of K greater than 4, this equation will have imaginary roots.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A chord of length 10 cm divides a circle of radius 5√2 cm in two segments. find the area of minor segment.

Answer:

Area of the shaded region is 100/7 sq cm.

In the given figure, OA = OB = 5√2 cm as they are the radii of the circle. Drop a perpendicular from O to the chord AB to instersect it at C. As we know, that a perpendicular from the center of a circle to a chord divides it into two parts of equal length, AC = CB = AB/2 = 5cm.
In right triangle OBC:
cos (angle OBA) = BC/OB = 5/5√2 = 1/√2 which gives us angle OBA = 45 degrees.
As OA = OB, angle opposite to them will be equal, i.e., angle OBA = angle OAB = 45 degrees.
Angle OAB + angle OBA + angle BOA = 180 (angle sum property of a triangle)
angle BOA = 180 - 2(45) = 180-90 = 90 degrees. Therefore, the angle of the sector is 90 degrees.
Therefore triangle OBA is a right triangle and so its area = 5√2*5√2/2 = 25*2/2 = 25 sq cm
Area of the sector = π*5√2*5√2*90/360 = 25π*2/4 = 25π/2 sq cm
Area of shaded region = Area of sector - Area of the triangle = 25π/2 - 25 = 25(π/2 - 1) = 25(11/7 - 1) = 25(4/7) = 100/7 sq cm


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

A solid cone of base radius 10cm is cut into two parts through mid points of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.

Answer:

The ratio of the volume of the frustum to volume of the cone is 7:1

We are given that AQ = QP = AP/2.
In triangle AQE and triangle APC:
angle AQE = angle APC = 90 degrees
angle AEQ = angle ACP (We are given that the cone is cut parallel to the base)
Therefore, triangle AQE is similar to triangle APC and AP/AQ = 2 = AC/AE = PC/QE .. (1)
Frustum DECB:
Height = QP
R1 = PC = 10cm
From (1), PC/QE = 2 we get QE = 5 cm
R2 = QE = 5 cm
Volume = (1/3)π*QP(10² + 5² + 10*5) = (1/3)π*QP(100+25+50) = (1/3)π*175QP
Cone ADE:
Height = AQ = QP
Radius = QE = 5cm
Volume = (1/3)π*QP(5²) = (1/3)π*25QP
Therefore, the ratio of their volumes:
= (1/3)π*175QP : (1/3)π*25QP
= 7:1


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

While boarding an aeroplane a passenger got hurt. The pilot showing promptness and concern made arrangements to hospitalise the injured and so the plane started late by 30 min. To reach the destination 1500 km away in time, the pilot increased the speed by 100 km/hr. Find the original speed/hour of the plane.

Answer:

The usual speed of the aeroplane is 500 kmph.

We are given that the distance = 1500 km
Let the time taken by the aeroplane at its usual speed be T hours and its usual speed be S kmph
Case 1(usual speed):
T = D/S = 1500/S ....(1)
Case 2(speed was increased):
Speed = (S+100) kmph
As the aeroplane left half an hour late and still reached the destination in time, time taken = (T - 1/2) hours
Therefore we have the equation:
T - 1/2 = D/(S+100) = 1500/(S+100)
From (1):
1500/S - 1/2 = 1500/(S+100)
⇒1500/S - 1500/(S+100) = 1/2
⇒1/S - 1/(S+100) = 1/3000
⇒(S+100-S)3000 = S(S+100)
⇒300000 = S^2 + 100S
⇒S^2 + 100S - 300000 = 0
⇒S^2+600S-500S-300000 = 0
⇒S(S+600)-500(S-600) = 0
⇒(S-500)(S+600) = 0
Therefore, either S = 500 or S = -600. Since speed of the aeroplane cannot be negative, we reject S = -600. Therefore, the usual speed of the aeroplane is 500 kmph.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

The 19th term of an AP is equal to three times its sixth term. If its 9th term is 19,find the AP.

Answer:

The AP is 3, 5, 7, 9, 11, ..............

We are given that the 19th term of the AP is 3 times its 6th term, i.e.,
a + (19-1)d = 3[a + (6-1)d]
⇒a + 18d = 3(a + 5d)
⇒a + 18d = 3a + 15d
⇒a + 8d = 3a + 5d
Now that we are given the 9th term to be 19, a + (9-1)d = 19 which implies that a + 8d = 19 ... (1)
Therefore,
19 = 3a + 5d
Now, (1) also implies that a = 19-8d. Substituting value of a in the above equation, we get:
19 = 3(19-8d) + 5d
⇒19 = 57 - 24d + 5d
⇒19 = 57 - 19d
⇒19d = 38
⇒d = 2

Going back to (1),
a + 8(2) = 19
⇒a + 16 = 19
⇒a = 3


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

In a figure O is the centre of a circle. PA and PB are tangents forom an external point P touching the circle at points A and B. If OP is equal to the diameter then prove that ABP is an equilateral triangle.

Answer:

Given:
OP = length of diameter of the cirlce, O is the center and PA and PB are the two tangents to the circle.
Proof:
OA and OB are the radii of the circle.
OP = length of diameter = 2(length of radius) = 2(OA) = 2(OB) ...(1)
angle PAO = angle PBO = 90 degrees (Angles between the radii and tangents)
PO is common and OA = OB (Radii of circle)
Therefore, triangle PAO is congruent to triangle PBO.
Since angle PAO is 90 degrees, triangle PAO is a right triangle. Therefore,
sinθ = OA/OP
From (1), we get:
sinθ = OA/2(OA)
sinθ = 1/2
Therefore, θ = 30 degrees and so angle OPB = 30 degrees (CPCTC). Therefore, angle APB = 60 degrees.
PA = PB (CPCTC). Therefore, angle PAB = angle PBA.
Angle PAB + angle PBA + angle APB = 180 (angle sum property of a triangle)
2(angle PAB) = 2(angle PBA) = 180 - 60
2(angle PAB) = 2(angle PBA) = 120 which gives us: angle PAB = angle PBA = 60 degrees.
As all the angles of the triangle measure 60 degrees, triangle APB is an equilateral triangle.
Hence, proved.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

There are 3 villages A,B and C such that the distance from A to B is 7Km, from B to C is 5 Km and from C to A is 8 Km. The gram pradhan wants to dig a well in such a way that the distance from each villages are equal. What should be the location of well?

Answer:

The distance from the villages to the well is [7√3]/3 km.

ABC forms a triangle with AB = 7km, BC = 5km and AC = 8km. The circumcenter of a triangle is equidistant from all its vertices as the three vertices lie on the circumcircle and so the distance from the circumcenter to any one of the vertices is its radius.
Semiperimeter of the triangle so formed = 8+7+5/2 = 20/2 = 10 km. Area of the triangle = sqrt[10(10-8)(10-7)(10-5)] = sqrt(10*2*3*5) = 10√3 sq km As we know,
Radius of the circumcircle = Product of the lengths of three sides/4(Area of triangle)
we have the distance from the villages to the well
= (8*7*5)/[4*10√3] = 7/√3 = 7√3/3 km


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

ABCD is a square with one side equal to 7cm. It consists of two quadrants ABC and BCD. Their point of intersection is P. Find the area of the shaded region.

Answer:

Area of the shaded region = 2.1266 sq cm.

Area of the shaded region = Area of square - (Area of the quadrant ABC + Area of quadrant BCD) + (Area of segment BQP + Area of segment CRP + Area of triangle CBP) ... (1)
Note: We are subtracting the middle area twice and that is why we have added that area in the end.

As we know ABC and BCD are quadrants, B is the center of the quadrant ABC and C is the center of the quadrant BCD. Therefore, radius of quadrant ABC = BC = 7cm and radius of quadrant BCD = CB = 7cm. Therefore, the two quadrants are congruent.
Join BP and CP. Since BP and CP are the radii of the two quadrants, BP = CP = BC = 7cm. Therefore, triangle BPC is an equilateral triangle with side = 7cm and so all of its interior angles are equal to 60 degrees, i.e., angle PBC = angle PCB = 60
Area of segment BQP:
= Area of sector CBP - Area of equilateral triangle CBP
= π*7*7*60/360 - 7*7√3/4
= (49/2)[π/3 - √3/2] sq cm
Similarly we get area of segment CRP = (49/2)[π/3 - √3/2] sq cm = Area of segment BQP
Sum of areas of the two segments = 2*(49/2)[π/3 - √3/2] = 49[π/3 - √3/2] sq cm
Area of triangle CBP = 7*7√3/4 = 49√3/4 sq cm
Area of quadrant ABC = Area of quadrant BCD = π*7*7*90/360 = π*7*7/4 = 49*π/4 sq cm
Sum of areas of the two quadrants = 2*49*π/4 = 49*π/2 sq cm
Area of square = 7*7 = 49 sq cm Therefore, area of the shaded region: [From (1)]
= 49 - (49*π/2) + (49[π/3 - √3/2] + 49*sqrt(3)/4
= 49[1 - π/2 + π/3 - √3/2 + sqrt(3)/4]
= 49[1 - π/6 - √3/4]
= 49[1 - 0.5236 - 0.433]
= 49[0.0434]
= 2.1266 sq cm.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

The sum of first q terms of an AP is 63q-3q² .If its pth term is -60,find the value of p. Also,find the 11th term of this AP.

Answer:

The pth term of the AP is 21 and the 11th term is 0.

If the sum of 'q' terms is (63q - 3q²),
Sum of 'p' terms = 63p - 3p² and the sum of 'p-1' terms = 63(p-1) - 3(p-1)²
As we know that difference between the sum of 'n' terms and sum of 'n-1' terms gives us the nth term,
(Sum of 'p' terms) - (Sum of 'p-1' terms) = pth term which is given to us to be -60.
Therefore, we have the equation:
63p - 3p² - [63(p-1) - 3(p-1)²] = -60
⇒ 63p - 3p² - 63(p-1) + 3(p-1)² = -60
⇒ 63p - 63(p-1) - 3p² + 3(p² + 1 -2p) = -60
Taking 63 and -3 common, we have:
⇒ 63[p-(p-1)] - 3[p²-(p²+1-2p)] = -60
⇒ 63(p-p+1) - 3(p²-p²-1+2p) = -60
⇒ 63(1) - 3(2p-1) = -60
⇒ 63-6p+3 = -60
⇒ 6p = 126
⇒ p = 21

Similarly, difference between the sum of 11 terms and (11-1) = 10 terms would give us the 11th term.
Therefore, the 11th term:
= 63(11) - 3(11)² - [63(10) - 3(10)²]
= 63(11) - 3(121) - 63(10) +3(100)
= 63(11-10) - 3(121-100)
= 63*1 - 3(21)
= 63 - 63
= 0


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Two water taps together can fill a tank in 75/8 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

Answer:

The two taps separately can fill the tank in 25 hours and 15 hours.

Let the time taken by the larger pipe to fill the tank be x hours.
Therefore, as the smaller tap takes 10 hours more to fill the tank, time taken by it to fill the tank will be (x+10) hours.
Portion of tank filled by the larger tap in 1 hour = 1/x and portion of tank filled by the smaller tap in 1 hour = 1/(x+10).
Therefore, portion of tank filled by them together in 1 hour = 1/x + 1/(x+10)
= (x+10+x)/x(x+10)
= (2x+10)/x(x+10)
If the two taps fill this much part in 1 hour, they would fill the tank in 1 * x(x+10)/(2x+10) hours which is given to us to be 75/8 hours. Thus, we have the following equation:
x(x+10)/(2x+10) = 75/8
⇒ (x²+10x)8 = 75(2x+10)
⇒ 8x²+80x = 75*2(x+5)
⇒ 4x²+40x = 75x+375
⇒ 4x²-35x-375 = 0
⇒ x²-35x/4-375/4 = 0
⇒ x²-60x/4+25x/4-375/4 = 0
⇒ x²-15x+25x/4-375/4 = 0
⇒ (x-15)x+(x-15)*25/4 = 0
⇒ (x-15)(x+25/14) = 0
Therefore, either x-15 = 0 in which case, x=15 or x+25/14 = 0 in which case, x=-25/14.
Since the number of hours taken cannot be negative, we reject x=-25/14. Thus, we get x = 15 and x+10 = 25.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

How can I unlock Legendary difficulty level in MotoGP2?

Answer:

To unlock legendary difficulty level, you have to win the championship on champion difficulty level.

Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Solve for x: 1/(x-1)(x-2) + 1/(x-2)(x-3) + 1/(x-3)(x-4) = 1/16.

Answer:

x = -2,7

Taking LCM of the first two terms:
(x-3)/(x-1)(x-2)(x-3) + (x-1)/(x-1)(x-2)(x-3) + 1/(x-3)(x-4) = 1/16
⇒(x-3+x-1)/(x-1)(x-2)(x-3) + 1/(x-3)(x-4) = 1/16
⇒(2x-4)/(x-1)(x-2)(x-3) + 1/(x-3)(x-4) = 1/16
⇒2(x-2)/(x-1)(x-2)(x-3) + 1/(x-3)(x-4) = 1/16
⇒2/(x-1)(x-3) + 1/(x-3)(x-4) = 1/16
Now, taking LCM of the remaining terms:
2(x-4)/(x-1)(x-3)(x-4) + (x-1)/(x-1)(x-3)(x-4) = 1/16
⇒(2x-8+x-1)/(x-1)(x-3)(x-4) = 1/16
⇒(3x-9)/(x-1)(x-3)(x-4) = 1/16
⇒3(x-3)/(x-1)(x-3)(x-4) = 1/16
⇒3/(x-1)(x-4) = 1/16
⇒(x-1)(x-4) = 18
⇒x²-5x+4 = 18
⇒x²-5x-14 = 0
⇒x²-7x+2x-14 = 0
⇒x(x-7)+2(x-7) = 0
⇒(x+2)(x-7) = 0
Therefore, either x+2 = 0 in which case x will be equal to -2 or x-7 = 0 in which x will be equal to 7.
Therefore, the vaule of x can be either -2 or 7.



Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If a/(a+b) = 15/21, then find (a+b)/(a-b).

Answer:

(a+b)/(a-b) = 7/3.

Given that:
a/(a+b) = 15/21 = 5/7 ...(1)
⇒ a/(a+b) - 1 = 5/7 - 1
⇒ (a-a-b)/(a+b) = (5-7)/7
⇒ -b/(a+b) = -2/7
Adding (1) to the above equation, we get:
-b/(a+b) + a/(a+b) = -2/7 + 5/7
⇒ (a-b)/(a+b) = 3/7
⇒ (a+b)/(a-b) = 7/3.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If the weight of a bucket full of water is 24 kg and weight of the bucket 1/4th full of water is 9 kg, then find the weight of the empty bucket.

Answer:

The weight of the empty bucket is 4 kg.

Let the weight of the empty bucket be x kg and weight of volume of water equal to volume of bucket be y kg and so weight of volume of water equal to one-fourth will be (y/4) kg.
Therefore, weight of bucket full of water = (x+y) kg = 24 kg ...(1)
And weight of the bucket 1/4th full of water = (x+y/4) kg = 9 kg which implies that 4x+y = 36 ...(2)
Subtracting (1) from (2):
(4x+y)-(x+y) = 36-24
⇒ 4x+y-x-y = 12
⇒ 3x = 12
⇒ x = 4
Therefore, we get the weight of the empty bucket equal to 4 kg.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If the mean weight of 8 people is increased by 4 when a person of weight 30 kg is replaced by another man, find the weight of the new man.

Answer:

The weight of the new man is 62 kg.

Let the mean of the 8 people be x kg.
Therefore, the sum of weights = 8x kg.
Let the weight of the new man be y kg.
When a person of weight 30 kg is replaced by the new man, the new sum of weights = (8x-30+y) kg.
Thus, the mean of the newly formed group which consists of 8 members = (8x-30+y)/8 which is given to be equal to x+4.
Therefore, we have the equation:
(8x-30+y)/8 = x+4
⇒ 8x-30+y = 8x+32
⇒ y = 32+30
⇒ y = 62
Therefore, we get the weight of the new man equal to 62 kg.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

It is proposed to add to a square lawn measuring 58 m on a side, two circular ends.The center of each circle being the point of intersection of the diagonals of the square.Find the area of the whole lawn.

Answer:

The area of the lawn is 4322.74 square meters.

Let ABCD be the square lawn and AED and BFC be the circular ends of the lawn.
AB = BC = CD = DA = 58 meters as ABCD is a square.
By applying Pythagoras Theorem in triangle BCD, we get:
(BD)² = (BC)² + (DC)² which implies that (BD)² = (58)² + (58)² which further implies that (BD)² = 2*(58)² and so we get BD equal to 58√2
As ABCD is a square, BD = 2CO = 2BO.
Therefore, OA = OC = BO = CO = BC/2 = 29√2 = Radius of the circular ends AED and BFC
angle AOD = angle BOC = 90° as diagonals of a square are perpendicular bisectors of each other.
Area of segment AED:
= Area of sector OAD - Area of triangle OAD
= πr²*θ/360 - OA*OD/2
= π*29*29*2*90/360 - 29*29*2/2
= 841(2π/4 - 1)
= 841(π/2 - 1)
= 841(π-2)/2 square meters
Similarly, we get area of segment BFC as 841(π-2)/2 square meters

Area of the entire lawn:
= Area of square lawn + Area of the two circular ends
= 58*58 + 2[841(π-2)/2]
= 29*29*4 + 841(π-2)
= 841(4+π-2)
= 841(2+π)
= 841(2+3.14)
= 841(5.14)
= 4322.74 square meters.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

What should be the position of an object relative to biconvex lens so that the lens behaves like a magnifying glass?

Answer:

The object should be placed between the focus and the optical center of the lens in order to make the lens behave like a magnifying glass.

When an object is placed between the focus and the optical center of a biconvex lens, the image formed is virtual, erect and magnified.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Find the sum of all three digits numbers each of which leave the remainder 3 when divided by 5.

Answer:

The sum of all three digits numbers each of which leave the remainder 3 when divided by 5 is 99090.

The smallest three digit number which leaves a remainder of 3 when divided by 5 is 100+3 = 103. The largest three digit number which leaves a remainder of 3 when divided by 5 is (1000-5)+3 = 998. Since all these numbers have a common difference, 5, they are in AP.
Let 998 be the nth term of the AP. Therefore,
103+(n-1)5 = 998 which implies that (n-1)5 = 895 which further implies that n-1 = 179 and this gives us n=180. Therefore, their sum is as follows:
180(103+998)/2 = 90(1101) = 99090.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

For what value of 'K' the numbers 3K + 2, 4K + 3 and 6K - 1 are the consecutive terms of an AP?

Answer:

Value of K is 5.

As 3K+2, 4K+3 and 6K-1 are in AP, (4K+3)-(3K+2) = (6K-1)-(4K+3) = common difference of the AP
Therefore, we have the equation:
4K+3-3K-2 = 6K-1-4K-3 which implies that K+1 = 2K-4 which further implies that K = 4+1 = 5.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If an aeroplane is flying horizontally at a height of 'h' meters from the ground and the angle of depressions of two consecutive kilometer stones(which are on either sides of the aeroplane) from the it are 'A' and 'B'. Then prove that: h = (tanA.tanB)/(tanA + tanB).

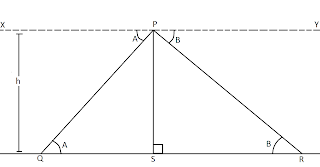
Answer:

The proof is given below.

Let P be the aeroplane and Q and R be the kilometer stones. PS is the height at which the aeroplane is flying. XY is the line of sight. Angle of depressions: angle XPQ = A and angle YPR = B.
Since XY and QR are horizontal, they ar parallel to each other. Therefore, we have angle PQS = A and angle PRS = B.

Since Q and R are two consecutive kilometer stones, QR = QS+SR = 1 km or SR = (1-QS) km .... (1)
In triangle PQS:
tanA = PS/QS which implies QS = PS/tanA .... (2)

In triangle PSR:
tanB = PS/SR which implies SR = PS/tanB.
From (1),
1-QS = PS/tanB which implies that 1 = PS/tanB + QS.
From (2),
1 = PS/tanB + PS/tanA which implies that 1 = (PS.tanA)/(tanA.tanB) + (PS.tanB)/(tanA.tanB) which further implies that 1 = (PS.tanA + PS.tanB)/(tanA.tanB). Taking PS common we get,
1 = PS(tanA + tanB)/(tanA.tanB) which implies that 1/PS = (tanA + tanB)/(tanA.tanB) which further implies that PS = (tanA.tanB)/(tanA + tanB).
Since PS is the height at which the aeroplane is flying, PS = h and so,
h = (tanA.tanB)/(tanA + tanB)

Hence proved.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

What is catenation?

Answer:

Catenation is the linkage of atoms of the same element to form longer chains.

Catenation is mainly observed in carbon. It forms covalent bonds with other carbon atoms to form longer structures.
The versatile chemistry of elemental sulfur is largely due to catenation. In the native state, sulfur exists as S8 molecules. On heating these rings open and link together giving rise to increasingly long chains, as evidenced by the progressive increase in viscosity as the chains lengthen. Selenium and tellurium also show variants of these structural motifs.


Please feel free to comment below for a detailed discussion.

Question

Coding for internal linking?

Answer:

Please click on the image for an enlarged view.


Please feel free to comment below for a detailed discussion.

Question

Coding for external linking?

Answer:

Please click on the image for an enlarged view.


Please feel free to comment below for a detailed discussion.

Question

What was the name of the first dog sent to the moon?

Answer:

Laika, a russian dog, was the first dog sent to space. There have been no animals to the moon yet.

The dog was launched into space on the Sputnik 2 in 1957. It survived the launch but after a week, the air ran out and Laika died.


Please feel free to comment below for a detailed discussion.

Question

The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?

Answer:

The new mean will be 15.

As we know the mean of 10 numbers is 20, the sum of the 10 numbers is 20*10=200. If 5 is subtracted from each number the new total would be 200-(10*5)=200-50=150 and hence, the new mean will be 150/10=15.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

The mean of 5 numbers is 18. If one of the numbers is excluded, their mean is 16. Then the excluded number is ___?

Answer:

The excluded number is 26.

Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

Find the co-ordinates of the point at which the perpendicular bisector of the line segment joining the points (1,5) and (4,6) cuts the y-axis.

Answer:

The co-ordinates of the point are (0,13).

P and Q are the given points. CD is the perpendicular bisector of PQ and C is the midpoint of PQ. We have to find the co-ordinates of D.
The slope of the line PQ is (6-5/4-1) = 1/3. As CD and PQ are perpendicular to each other the product of their slopes will be equal to -1. Therefore, slope of line CD = -3.
The co-ordinates of C are (5/2,11/2) [By the section formula]
Therefore, we have the equation:
(11/2-y)/(5/2-0) = -3 which implies (11-2y)/5 = -3 which further implies 11-2y = -15 which implies that 2y = 26 and thus, we get y = 13.
Therefore, the co-ordinates of the required point is (0,13).


Please feel free to comment below for a detailed discussion/worked out solution to this problem.

Question

If z = x + iy, then |2z - i| / |z + 1| = m represents a circle when m is not equal to ____?

Answer:

m is not equal to ±2

The radius of the circle tends to infinity when m is ±2


Please feel free to comment below for a detailed discussion/worked out solution to this problem.