Question

If an aeroplane is flying horizontally at a height of 'h' meters from the ground and the angle of depressions of two consecutive kilometer stones(which are on either sides of the aeroplane) from the it are 'A' and 'B'. Then prove that: h = (tanA.tanB)/(tanA + tanB).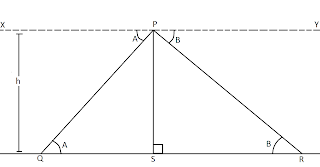

Answer:

The proof is given below.

Let P be the aeroplane and Q and R be the kilometer stones. PS is the height at which the aeroplane is flying. XY is the line of sight. Angle of depressions: angle XPQ = A and angle YPR = B.
Since XY and QR are horizontal, they ar parallel to each other. Therefore, we have angle PQS = A and angle PRS = B.

Since Q and R are two consecutive kilometer stones, QR = QS+SR = 1 km or SR = (1-QS) km .... (1)
In triangle PQS:
tanA = PS/QS which implies QS = PS/tanA .... (2)

In triangle PSR:
tanB = PS/SR which implies SR = PS/tanB.
From (1),
1-QS = PS/tanB which implies that 1 = PS/tanB + QS.
From (2),
1 = PS/tanB + PS/tanA which implies that 1 = (PS.tanA)/(tanA.tanB) + (PS.tanB)/(tanA.tanB) which further implies that 1 = (PS.tanA + PS.tanB)/(tanA.tanB). Taking PS common we get,
1 = PS(tanA + tanB)/(tanA.tanB) which implies that 1/PS = (tanA + tanB)/(tanA.tanB) which further implies that PS = (tanA.tanB)/(tanA + tanB).
Since PS is the height at which the aeroplane is flying, PS = h and so,
h = (tanA.tanB)/(tanA + tanB)

Hence proved.


Please feel free to comment below for a detailed discussion/worked out solution to this problem.